小林晋平著、「宇宙の見え方が変わる物理学入門」、ベレ出版、2021を読んでいて、「最小作用の原理って面白い!」と思ったので書いておきたいと思います。
【2点間の最短距離】
空間に2点の点A, 点Bがある時、その2点を結ぶ最短の線分は、直線ですよね。
では、図のようにその点Aと点Bに加えてある面Sがあったとき、点Aから一度面Sにタッチして点Bに行く場合の最短の線分はどうなるでしょうか?

私の答えは、光の反射みたいに、点Aから面Sに入る入射角と面Sから点Bに向かう反射角が等しくなる点だと思いました。
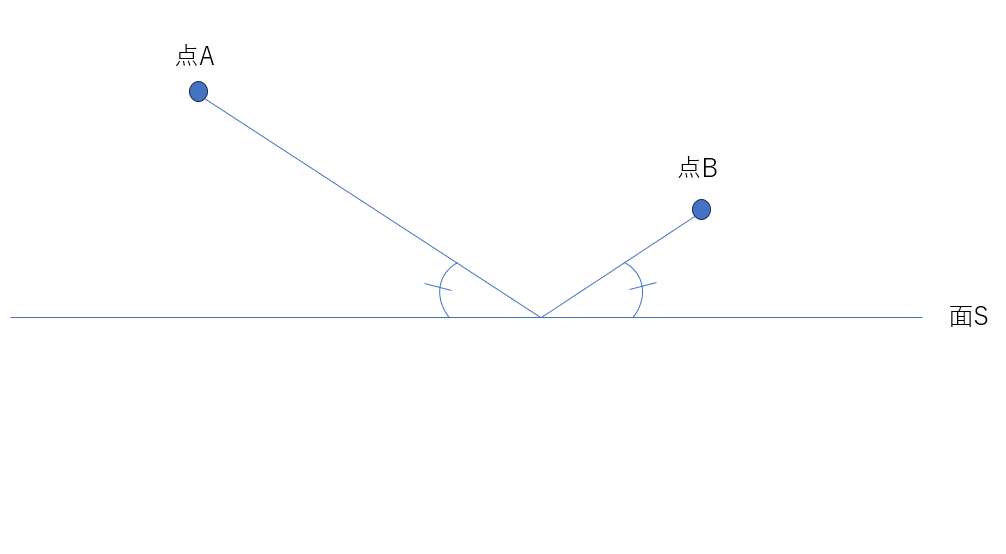
間違いではないのですが、もっと簡単にイメージする方法がありました。
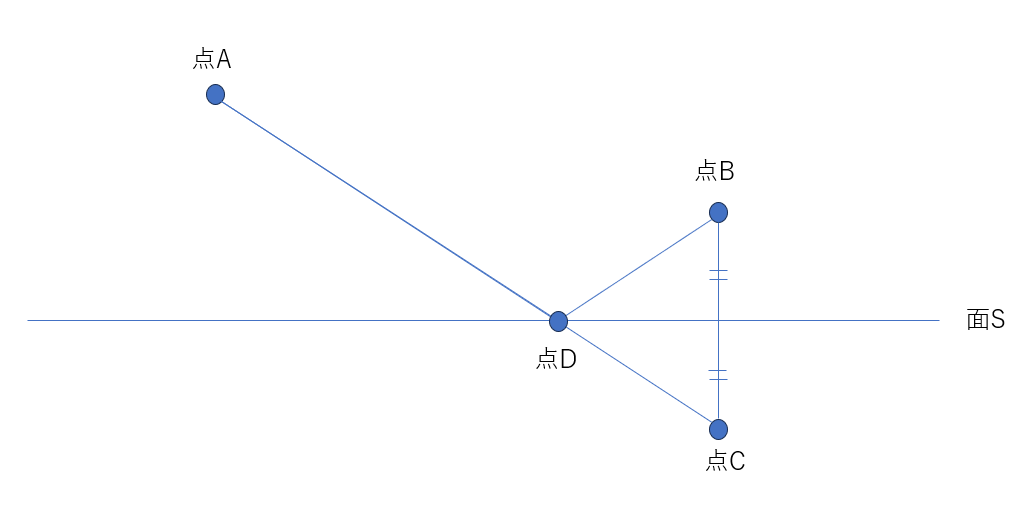
点Bから面Sに垂線を下して、点Bから面Sまでに距離と同じ距離のところに点Cを設けて、点Aと点Cを直線で結びます。線分ACと面Sの交点を点Dとして、点Dと点Bを線で結びます。
したがって、質問「点Aから一度面Sにタッチして点Bに行く場合の最短の線分」の答えは、
折れ線ADBとなります。
【3点間の最短距離】
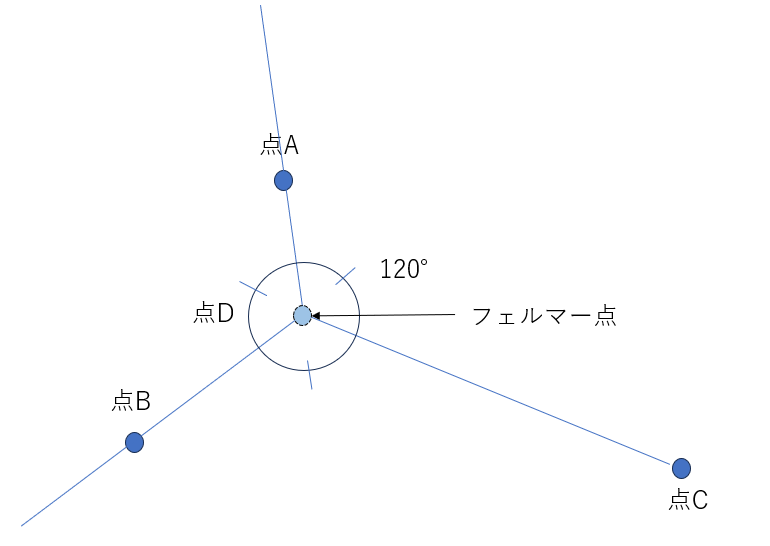
では、次の3点、点A、点B、点Cと同一面上に点Dを設ける際に、線分AD+線分BD+線分CDが最短になる点Dはどこになるでしょうか?

答えは、∠ADB=∠BDC=∠CDA=120°となる点Dです。この点Dのような点をフェルマー点というそうです。
【4点間の最短距離】
次に4点の場合はどうでしょうか?

答えは以下のように、フェルマー点が2つできるそうです。
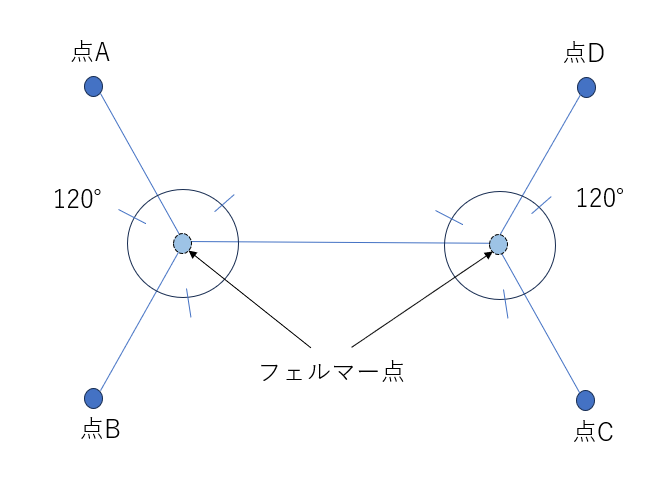
ちなみに、点A~点Dを棒にしてその棒を透明のアクリルにで上下を挟んで、シャボン液につけて、ゆっくり上げると、シャボン液の表面張力で上記のような膜ができるそうです。面白い!!
また、この形をシュタイナーツリーと呼ぶそうです。
【立方体の格子点の最短距離】
同じようにして、点を立方体に配置したらどうなるでしょうか?
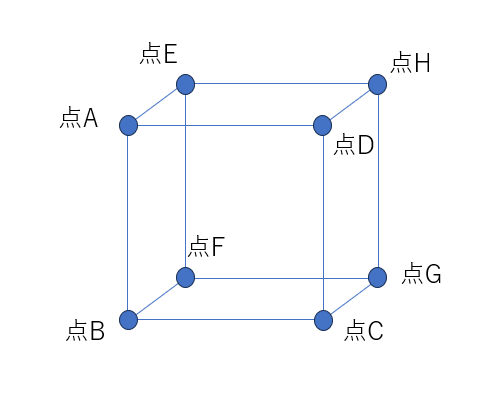
答えは・・・。針金で上記のような骨組みを作ってシャボン液につけると、出てくるそうです。
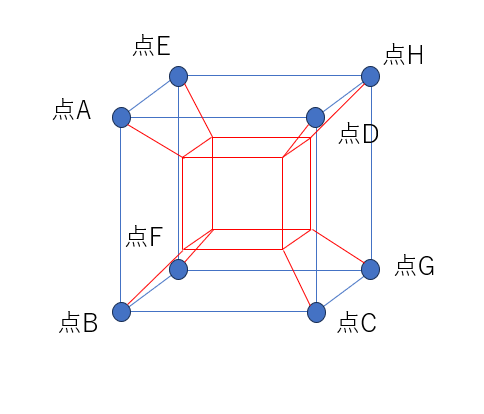
こんな感じになるのかな?中央は立方体ではないかも・・・。やってみてください。
私もやる気になったら、試してみたいと思います。
【まとめ】
最小作用の原理の距離に関する例は、記述した通りです。
立体に関する距離の最小化は、シャボン液の膜を使うと、表面張力自体が面を最小に保とうとするので、簡単に見れるとのこと。
これから始まる夏休みの自由研究にしてもおもしろそうですね。



コメント